We have already learned to represent the integers, such as 0, 1, 2, -1, -2, on a number line. In the same way, we can represent fractions on a number line.
For example, if we have to represent 1/5 and 3/5 parts of a whole, then it can be represented as shown in the below figure.
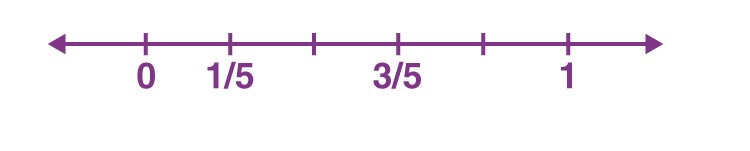
Since the denominator is equal to 5, thus 1 is divided into 5 equal parts, on the number line. Now the first section is 1/5 and the third section is 3/5.
Similarly, you can practice marking more of the fractions on the number line, such as 1/2, 1/4, 2/11, 3/7, etc.
Rules for Simplification of Fractions
There are some rules we should know before solving the problems based on fractions.
Rule #1: Before adding or subtracting fractions, we should make sure that the denominators are equal. Hence, the addition and subtraction of fractions are possible with a common denominator.
Rule #2: When we multiply two fractions, then the numerators are multiplied as well as the denominators are multiplied. Later simplify the fraction.
Rule #3: When we divide a fraction from another fraction, we have to find the reciprocal of another fraction and then multiply with the first one to get the answer.
Adding Fractions
The addition of fractions is easy when they have a common denominator.
For example, ⅔ + 8/3 = (2+8)/3 = 10/3
Hence, we need to just add the numerators here.
Adding Fractions with Different Denominators
If the denominators of the two fractions are different, we have to simplify them by finding the LCM of denominators and then making it common for both fractions.
Example: ⅔ + ¾
The two denominators are 3 and 4
Hence, LCM of 3 and 4 = 12
Therefore, multiplying ⅔ by 4/4 and ¾ by 3/3, we get;
8/12 + 9/12
= (8+9)/12
Subtracting Fractions
The rule for subtracting two or more fractions is the same as for addition. The denominators should be common to subtract two fractions.
Example: 9/2 – 7/2 = (9-7)/2 = 2/2 = 1
Subtracting with Different Denominators
If the denominators of the two fractions are different, we have to simplify them by finding the LCM of denominators and then making it common for both fractions.
Example: ⅔ – ¾
The two denominators are 3 and 4
Hence, LCM of 3 and 4 = 12
Therefore, multiplying ⅔ by 4/4 and ¾ by 3/3, we get;
8/12 – 9/12
= (8-9)/12
Multiplication of Fractions
As per rule number 2, we have discussed in the previous section, when two fractions are multiplied, then the top part (numerators) and the bottom part (denominators) are multiplied together.
If a/b and c/d are two different fractions, then the multiplication of a/b and c/d will be:
(a/b) x (c/d) = (axc)/(bxd) = (ac/bd)
Example: Multiply ⅔ and 3/7.
(⅔) x (3/7) = (2×3)/(3×7) = 2/7
Division of Fractions
If we have to divide any two fractions, then we will use here rule 3 from the above section, where we need to multiply the first fraction to the reciprocal of the second fraction.
If a/b and c/d are two different fractions, then the division a/b by c/d can be expressed as:
(a/b)÷(c/d) = (a/b)x(d/c) = (ad/bc)
Example: Divide ⅔ by 3/7.