A perimeter of a triangle is defined as the total length of the outer boundary of the triangle. Or we can say, the perimeter of the triangle is equal to the sum of all its three sides. The unit of the perimeter is same as the unit of sides of the triangle.
| Perimeter = Sum of All Sides |
If ABC is a triangle, where AB, BC and AC are the lengths of its sides, then the perimeter of ABC is given by:
Area of a Triangle
The area of a triangle is the region occupied by the triangle in 2d space. The area for different triangles varies from each other depending on their dimensions. We can calculate the area if we know the base length and the height of a triangle. It is measured in square units.
Suppose a triangle with base ‘B’ and height ‘H’ is given to us, then, the area of a triangle is given by-
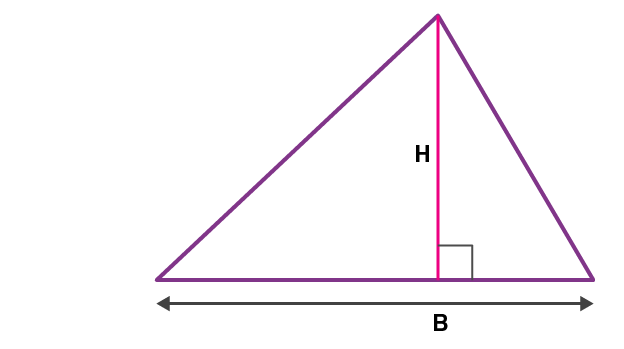
Formula:
| Area of triangle = Half of Product of Base and HeightArea = 1/2 × Base × Height |
Example
Question- Find the area of a triangle having base equal to 9 cm and height equal to 6 cm.
Solution- We know that Area = 1/2 × Base × Height
= 1/2 × 9 × 6 cm2
= 27 cm2
Area of Triangle Using Heron’s Formula
In case, if the height of a triangle is not given, we cannot be able to use the above formula to find the area of a triangle.
Therefore, Heron’s formula is used to calculate the area of a triangle, if all the sides lengths are known.
First, we need to calculate the semi perimeter (s).
s = (a+b+c)/2, (where a,b,c are the three sides of a triangle)
Now Area is given by; A = √[s(s-a)(s-b)(s-c)]
Solved Examples
Question 1: If ABC is a triangle where AB = 3cm, BC=5cm and AC = 4cm, then find its perimeter.
Solution: Given, ABC is a triangle.
AB = 3cm
BC = 5cm
AC = 4cm
As we know by the formula,
Perimeter = Sum of all three sides
P = AB + BC + AC
P = 3+5+4
P = 12cm
Question 2: Find the area of a triangle having sides 5,6 and 7 units length.
Solution- Using Heron’s formula to find the area of a triangle-
Semiperimeter (s) = (a+b+c)/2
s = (5 + 6 +7)/2
s = 9
Now Area of a triangle = √[s(s-a)(s-b)(s-c)]
=√[9(9-5)(9-6)(9-7)]
=√ [9 × 4 × 3 × 2]
=√ [3 × 3 × 2 × 2 × 3 × 2]
=√ [32 × 22 × 3 × 2]
= 6√6 square units.